Recursive SQL queries in Feldera

The latest update to the Feldera SQL compiler adds support for a major feature: recursive queries. The SQL language has offered support for recursive queries since the SQL 99 standard. The standard definition has several problems:

• the syntax is cumbersome, making it difficult to remember and use
• it imposes severe restrictions on the nature of recursive queries
• it has very unusual semantics

Problems of the standard definition have been well described elsewhere; a great summary can be found in Frank McSherry's blog post about recursion.

In this blog post we describe Feldera's design for recursion, which addresses all these shortcomings.

Not only our design and implementation addresses the above shortcomings, but the implementation is also incremental (as is the rest of the Feldera engine). We have described incremental database computations in a separate blog post. Incremental evaluation is an algorithm which evaluates queries directly on the input and output changes, without recomputing each query on the full input dataset whenever a change occurs. But in this post we do not talk about how incremental evaluation is achieved for recursive queries; that will be the subject of a future post.

Our implementation is still considered experimental, which means that some features may change before they are stabilized.

A new syntax for (mutually) recursive views

Choosing to implement a major SQL feature in a way which is incompatible with the standard sounds like a bad idea. However, in this case we consider the standard definition irremediably broken. Rather than trying to pretend that we are implementing the standard definition, we have chosen to use a completely different syntax, to make it clear that our implementation is incompatible with the standard. We have also chosen not to support the standard syntax at all.

Standard SQL has very limited support for recursive computations using common-table expressions. The standard definition is both difficult to use, and lacks expressiveness. Feldera SQL uses an alternative syntax for defining recursive SQL computations, which is easier to use and significantly more powerful. Our syntax:

• does not require common-table expressions
• allows mutually-recursive view definitions involving any number of views
• allows much richer queries for defining recursive views, including non-monotone queries.

Designing new programming language feature is a very difficult subject, and can often produce wrong designs. So we have decided to base our design on a time-tested solution. Our syntax is based on the C language.

In C one writes recursive functions by using forward declarations. In a C program the forward declarations have to occur before the actual function definitions.

For example, to write functions f and g that invoke each other, one
first writes the declaration(s), then the definitions:

/* Forward declaration of function g */
int g(int x);

/* Definition of function f */
int f(int x) {
... g(n-1); /* f calling g */
}

/* Definition of function g */
int g(int x) {
... f(n-1); /* g calling f */
}

Similarly to C, we introduce the notion of forward view declaration. A forward view declaration is similar to a table CREATE statement (but without constraints on columns, like primary keys). The declaration specifies the view name and
the columns and their types, as in the following example:

DECLARE RECURSIVE VIEW CLOSURE(x int, y int);

Each view that is used in a query before being defined needs a forward declaration. The forward declaration must occur before the view definition in the program. (One can provide forward declarations for non-recursive views, but they are of limited utility; that's why the declaration always has the keyword RECURSIVE).

Given a forward declaration, a recursive view can be defined using the standard SQL syntax. The forward declaration allows the view query to depend on the view itself:

CREATE TABLE EDGES(x int, y int);
-- a local view that depends on CLOSURE and EDGES 
CREATE LOCAL VIEW STEP AS SELECT EDGES.x, CLOSURE.y FROM EDGES JOIN CLOSURE ON EDGES.y = CLOSURE.x
-- actual definition of view CLOSURE, which depends on STEP and E 
CREATE MATERIALIZED VIEW CLOSURE AS (SELECT * FROM EDGES) UNION (SELECT * FROM STEP);

In the above SQL example the EDGES table represents the edges of a graph where nodes are integers. The CLOSURE view represents the edges of a graph over the same nodes, such that CLOSURE is the transitive closure of the EDGES graph. Notice how the definition of the view CLOSURE uses the view STEP, which in turn uses the view CLOSURE.

Languages like Java do not require recursive functions to be declared. Could we have simplified the syntax even further? Perhaps. But there is a notable difference between SQL views and SQL tables: while tables have their schema explicitly specified (by listing the names and types of all columns), in SQL the schema of a view is inferred from the query defining the view. Thus, without explicit declarations, the compiler's job for computing the type of a view's columns becomes much harder, and possibly even under-specified (i.e., there could be multiple types that could satisfy a given recursive definition). So we have chosen the pragmatic solution of requiring forward declarations. These enable the compiler to provide better error diagnostics and significantly simpler compilation algorithms.

Semantics

What does a recursive query compute?

In other programming languages we are used to seeing statements like x = x + 1. For a mathematician this looks like an equation without any solution, but programmers know that this means "the next value of x will be 1 more than the current value of x". The same interpretation is given to recursive views in a SQL query. When we compute a view using a query that refers to the view itself, we are computing the next value of the view.

In our current implementation the compiler treats each recursive view as a DISTINCT query, even if the DISTINCT keyword is not used. In our example the CLOSURE view is defined by a UNION operation, which always implies a DISTINCT. However, the view would have the exact same meaning even if we used UNION ALL in the query. This is a pragmatic choice (which we may decide to undo in a future iteration of the language design).

To evaluate a program with recursion, the following algorithm is used:

• Each group of mutually-recursive views is evaluated together. (More precisely, the compiler builds a dependence graph of all views, and all views that are in the same strongly connected component are evaluated together).
• The non-recursive parts of the program are evaluated using standard SQL evaluation
• To evaluate a recursive component the following algorithm is used:
  • all recursive views are initialized to the empty set
  • repeat
    • compute the next value for all recursive views using standard SQL evaluation (treating the query defining the views as if it is not recursive)
    • if next value = current value for all views, stop the loop

Example

Let us consider the evaluation of our example program when the input table EDGES contains a collection with two pairs, in SQL this can be denoted by VALUES ((1,2), (2,3)).

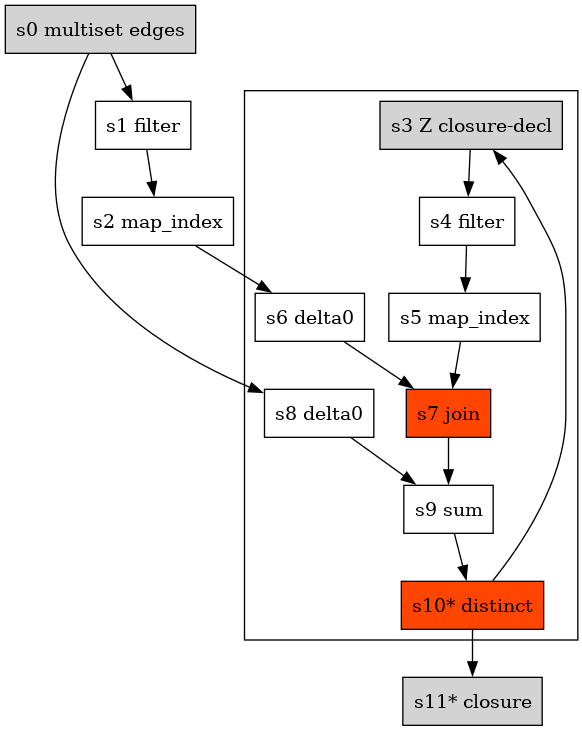
The dataflow graph of the program as represented in the compiler is:

In this diagram CLOSURE_DECL is the current value of view CLOSURE, and CLOSURE is the next value of the view.

At runtime evaluation proceeds as follows:

• CLOSURE_DECL is initialized to contain the empty multiset
• Iteration 1:
  • The content of the STEP view is evaluated, it is the JOIN of EDGES with CLOSURE_DECL, which produces an empty multiset
  • CLOSURE is evaluated, it is the UNION of STEP and EDGES, which is the same as EDGES, since STEP is empty.
  • Since CLOSURE_DECL is different from CLOSURE, evaluation of the recursive component is repeated. CLOSURE_DECL is set to contain the current value of CLOSURE, which is ((1,2), (2,3))
• Iteration 2:
  • STEP is evaluated as the join of EDGES with CLOSURE_DECL which yields ((1,2),(2,3),(1,3))
  • CLOSURE is evaluated as the UNION of STEP and EDGES, which is ((1,2),(2,3),(1,3)). Notice that because STEP is a result of a DISTINCT UNION there are no duplicates. (Without the DISTINCT, STEP would contain ((1,2),(1,2),(2,3),(2,3),(1,3))).
  • Since CLOSURE_DECL is different from CLOSURE, evaluation of the recursive component is repeated. CLOSURE_DECL is set to contain the current value of CLOSURE, which is ((1,2),(2,3),(1,3))
• Iteration 3:
  • STEP is evaluated as the join of EDGES with CLOSURE_DECL, which yields the same value as in Iteration 2: ((1,2),(2,3),(1,3))
  • CLOSURE is evaluated as the UNION of STEP and EDGES, which is ((1,2),(2,3),(1,3)).
  • Since CLOSURE_DECL is the same as CLOSURE, evaluation of the recursive component is now completed.

This is the final result produced by the program for this input.

This result is also called the least fixed point of the query for a given input. It is called "least" because the result starts from the smallest possible value, which is the empty set for all recursive views. It is called a "fixed point" because the loop stops when nothing changes. There is no point in repeating the loop anymore, since the outputs will never change from this point on.

This semantics of the set of mutually recursive views is the most natural mathematical definition. All programming languages use a definition which is essentially equivalent mathematically. Interestingly, the SQL standard specifies a result for the recursion which is not the least fixed point, which is one big reason the definition is considered broken.

Restrictions? What restrictions?

There are very few restrictions on the queries that can define mutually recursive views in Feldera. Currently we do not allow window queries using OVER statements, but we hope to remove this restriction at some point as well.

You can use aggregates, GROUP BY, JOIN, DISTINCT, UNION, EXCEPT, INTERSECT, etc., pretty much all standard SQL operators that are supported in non-recursive Feldera SQL queries.

In standard SQL the shape of the queries is restricted to produce only monotone results, where the contents of each recursive view has more tuples at every iteration. Feldera allows non-monotone queries as well. In this respect, Feldera SQL should be able to express all programs that can be written in Datalog-like languages.

With great power comes great responsibility. Since recursive queries can be much more powerful, it is possible to write queries that never terminate (but this was already possible in standard SQL as well). Currently there is no built-in mechanism for detecting and stopping such run-away queries, but we are designing some solutions.

Conclusions

Recursion in standard SQL is broken. But there is nothing in the SQL language design which prevents a "sane" design and implementation of recursion. We believe that the Feldera's version is much easier to understand and to use than alternatives, and it is also much more useful. In future blog posts we plan to show many examples that can be only written using recursive queries.