Queries using Z-sets

We have introduced Z-sets in the previous post. In this post we write some Java code which implements ZSets, to (1) show how simple they are and (2) to make it completely clear how they work. (The DBSP runtime provided by Feldera is implemented in Rust, and provides similar functionality using specialized data structures optimized for performance.)

Today we build the primitive operations that compute on Z-sets. In a future post we will see how we can use these primitive operations to perform traditional database computations using Z-sets.

Z-Sets summary

Recall that a Z-Set is a collection of values where each value has an attached integer weight. The weights can be positive or negative. If a value has a zero weight we say that it does not belong to the collection. (Our implementation supports non-integer weights as well, but we will stick to integers for now.)

The values in a Z-set are usually the rows that would belong to a database table.

In Java one could represent a Z-set as a Map<Row, Integer>.

Such a representation has an important shortcoming: unlike mathematical integers, Java integers only use 32 bits. With int we cannot represent multisets where an element appears more than 2 billion times. While this may seem enough for many practical applications, it turns out that computing on Z-sets can sometimes produce intermediate results with very large weights, so this can be a real problem in practice. Overflows can lead to runtime exceptions, or, even worse, to silently corrupted results.

Abstracting weights

In order to be future-proof, let's create first an abstraction for the weights:

public interface WeightType<T> {
    T add(T left, T right);
    T negate(T value);
    T zero();
    T one();
    boolean isZero(T left);
    boolean greaterThanZero(T value);
    T multiply(T left, T right);
  }

This is an interface describing a type of weights. The actual weights are implemented by type T. A weight type must have a zero value, it needs to be able to add and negate weights.

The concept of a weight with value 1 is important, so it has its own method. We will also see that there are cases where weights need to be multiplied (spoiler: for implementing database joins). Finally, we need to be able to compare weights with zero, and to check whether weights are positive.

Here is an implementation of this interface using Integers with checked operations that throw an exception on overflow:

public class IntegerWeight implements WeightType<Integer> {
    private IntegerWeight() {}

    public static IntegerWeight INSTANCE = new IntegerWeight();

    @Override
    public Integer add(Integer left, Integer right) {
        return Math.addExact(left, right);
    }

    @Override
    public Integer negate(Integer value) {
        return Math.negateExact(value);
    }

    @Override
    public Integer zero() {
        return 0;
    }

    @Override
    public Integer one() { return 1; }

    public boolean isZero(Integer value) {
        return value == 0;
    }

    @Override
    public boolean greaterThanZero(Integer value) {
        return value > 0;
    }

    @Override
    public Integer multiply(Integer left, Integer right) {
        return Math.multiplyExact(left, right);
    }
}

This implementation of weights is not cheap, since it uses a boxed integer (a Java object, allocated on the heap) for every tuple in a table. Rust can be much more efficient, since it does not use objects, but traits, which can be implemented even for existing compact datatypes such as integers.

Implementing Z-sets

Here is a preliminary implementation of Z-sets in Java:

public class ZSet<Data, Weight> {
    /** Maps values to weights. Invariant: weights are never zero */
    final Map<Data, Weight> data;
    final WeightType<Weight> weightType;

    public ZSet(Map<Data, Weight> data, WeightType<Weight> weightType) {
        this.data = data;
        this.weightType = weightType;
        for (Map.Entry<Data, Weight> datum: data.entrySet()) {
            if (!this.weightType.isZero(datum.getValue()))
                this.data.put(datum.getKey(), datum.getValue());
        }
    }

    /** Create an empty Z-set */
    public ZSet(WeightType<Weight> weightType) {
        this.data = new HashMap<>();
        this.weightType = weightType;
    }

    public int entryCount() {
        return this.data.size();
    }

    public boolean isEmpty() {
        return this.data.isEmpty();
    }

    @Override
    public String toString() {
        StringBuilder result = new StringBuilder();
        result.append("{\n");
        for (Map.Entry<Data, Weight> entry: this.data.entrySet()) {
            result.append(entry.getKey());
            result.append(" => ");
            result.append(entry.getValue());
            result.append("\n");
        }
        result.append("}");
        return result.toString();
    }
}

We have refrained from defining a size() method for Z-sets, since its meaning would be ambiguous: what is the size of a Z-set with two rows, one with weight 1 and the other with weight -1? Instead, we have entryCount(), which is the number of entries with non-zero weights.

What is implicit in this code is that the type Data must have good implementations for equals() and hashCode(), since it is used as key in a HashMap.

Converting tables to and from Z-sets

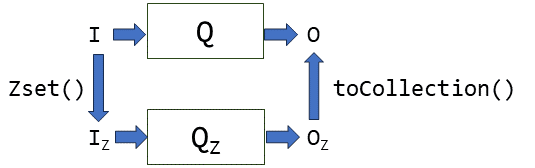
Database queries compute on the contents of tables (or views). (Theoreticians call both tables and views "relations".) For any query Q that a user can write that computes on relations, one can write another query QZ that computes on Z-sets and produces the "same" result. To explain what "same" means we need a way to convert tables (more generally, collections), into Z-sets and back.

Converting a collection to a Z-set

To convert a collection into a Z-set we essentially attach a weight of 1 to every value in the collection. If the collection contains repeated values, their weights will be added. So a Set collection will be translated into a Z-set where all weights are 1. A multiset collection will be translated into a Z-set where all weights are positive. (Recall that a multiset can have multiple copies of a value.)

Let's define some methods to add data to a Z-set:

public class ZSet<Data, Weight> {
    // ... extending previously defined class

    public ZSet(Collection<Data> data, WeightType<Weight> weightType) {
        this.data = new HashMap<>();
        this.weightType = weightType;
        for (Data datum: data)
            this.data.merge(datum, this.weightType.one(), this::merger);
    }

    /** Add two weights, return null if the result is 0. */
    @Nullable
    Weight merger(Weight oldWeight, Weight newWeight) {
        Weight w = this.weightType.add(oldWeight, newWeight);
        if (this.weightType.isZero(w))
            return null;
        return w;
    }

    public ZSet<Data, Weight> append(Data data, Weight weight) {
        this.data.merge(data, weight, this::merger);
        return this;
    }

    public ZSet<Data, Weight> append(Data data) {
        this.append(data, this.weightType.one());
        return this;
    }
}

We have used several times in the code the Map.merge method to update the weight of an existing key in the data map. We always call merge using our helper method ZSet.merger. The merger method adds two weights, but returns null when the result is 0. When the Map.merge method receives a null from the merger it removes the corresponding key from the Zset.data map. This is how we enforce the invariant that no data values with 0 weight are present in the ZSet.data map.

Converting Z-sets to collections

It is less clear how to convert a Z-set to a collection. If all weights are positive it's not so difficult, but what should we do for negative weights?

We define a handy function, called positive, which ensures that all entries in a Z-set have positive weights:

public class ZSet<Data, Weight> {
    // ... extending previously defined class
    public ZSet<Data, Weight> positive(boolean set) {
        Map<Data, Weight> result = new HashMap<>();
        for (Map.Entry<Data, Weight> entry: this.data.entrySet()) {
            Weight weight = entry.getValue();
            if (!this.weightType.greaterThanZero(weight))
                continue;
            if (set)
                weight = this.weightType.one();
            result.put(entry.getKey(), weight);
        }
        return new ZSet<>(result, this.weightType);
    }

    public ZSet<Data, Weight> distinct() {
        return this.positive(true);
    }
}

The positive method produces a Z-set representing either a set (if the argument is true) or a multiset (if the argument is false). In both cases it throws away entries with negative weights. In the former case, it truncates all positive weights to 1. We provide a convenience method called distinct which always returns a Z-set representing a set.

Finally, we can implement the arithmetic operations on Z-sets that we described in our previous blog post, addition, negation, subtraction. These operate simply on the weights, and do not care much about the data itself.

public class ZSet<Data, Weight> {
    // ... extending previously defined class
    public ZSet<Data, Weight> negate() {
        Map<Data, Weight> result = new HashMap<>();
        for (Map.Entry<Data, Weight> entry: this.data.entrySet()) {
            result.put(entry.getKey(), this.weightType.negate(entry.getValue()));
        }
        return new ZSet<>(result, this.weightType);
    }

    public static <Data, Weight> ZSet<Data, Weight> zero(WeightType<Weight> weightType) {
        return new ZSet<>(weightType);
    }

    public ZSet<Data, Weight> add(ZSet<Data, Weight> other) {
        Map<Data, Weight> result = new HashMap<>(this.data);
        for (Map.Entry<Data, Weight> entry: other.data.entrySet()) {
            result.merge(entry.getKey(), entry.getValue(), this::merger);
        }
        return new ZSet<>(result, this.weightType);
    }

    public ZSet<Data, Weight> subtract(ZSet<Data, Weight> other) {
        Map<Data, Weight> result = new HashMap<>(this.data);
        for (Map.Entry<Data, Weight> entry: other.data.entrySet()) {
            result.merge(entry.getKey(), this.weightType.negate(entry.getValue()), this::merger);
        }
        return new ZSet<>(result, this.weightType);
    }
}

This implementation is purely functional: when you add two Z-sets you get a new one. In practice one would also add methods that mutate Z-sets.

Interestingly, with these notions of 0, plus (add), and minus (subtract), Z-sets form the algebraic structure of a "commutative group". The Z-sets inherit the group structure from the integer numbers ℤ, that is a very fundamental mathematical property. In general a datatype B has a nice algebraic structure (e.g., it's a group), then one can naturally define the same algebraic structure for Map<A, B>, no matter what the type A is. The group structure is actually a fundamental property of the data required by DBSP in order to define its notion of incremental computation.

Does it work?

Yes, this implementation works correctly (modulo bugs), and our initial implementation in Rust paralleled this structure quite closely. Moreover, this implementation is algorithmically pretty good. However, we have also discovered that in practice it is very slow. How can be it be algorithmically good and still slow? Well, the asymptotic costs (the O(n) stuff you learned in the algorithms class) are good, but the constant factors are bad. Our initial implementation was about 10x slower than we expected. The fundamental reason is that these hashmaps have very poor cache locality. Our actual implementation in Rust is much more complicated, and it is based on the Differential Dataflow implementation, which in turn is based on concepts from log-structured merge trees. But that's a subject for another blog post.

In the next post in this series we show how SQL operations work on Z-sets.

Footnotes

1. Because Java interfaces cannot contain static methods we have created an interface for the type of weights, and not for the weights themselves. This way we can have a zero method. Rust traits have no such limitations, but the trait that we use for weights is built from many other simpler traits so it's not so easy to summarize.