Solving Fine-Grained Authorization by Turning the Problem on its Head

If you've been following the security space, you've likely noticed the rise of Fine-Grained Authorization (FGA) access control models. An access control model determines who can access an application and what actions they are allowed to perform. These models often need to be tailored to the specific needs of an application. FGA provides a principled way to build application-specific access control models, while keeping the authorization logic separate from the application logic. With FGA, developers write application-specific access control rules using a declarative language. The FGA engine enforces these rules dynamically at runtime.
First popularized by Google's Zanzibar system, FGA now has numerous implementations, including open-source and commercial solutions.
Like any powerful abstraction, FGA can be an expensive one to implement. At the core of any FGA platform lies a compute engine that evaluates FGA rules in real-time. In a large system this engine must evaluate thousands of requests per second over an object graph with millions of objects. Each authorization request can require an expensive graph traversal.

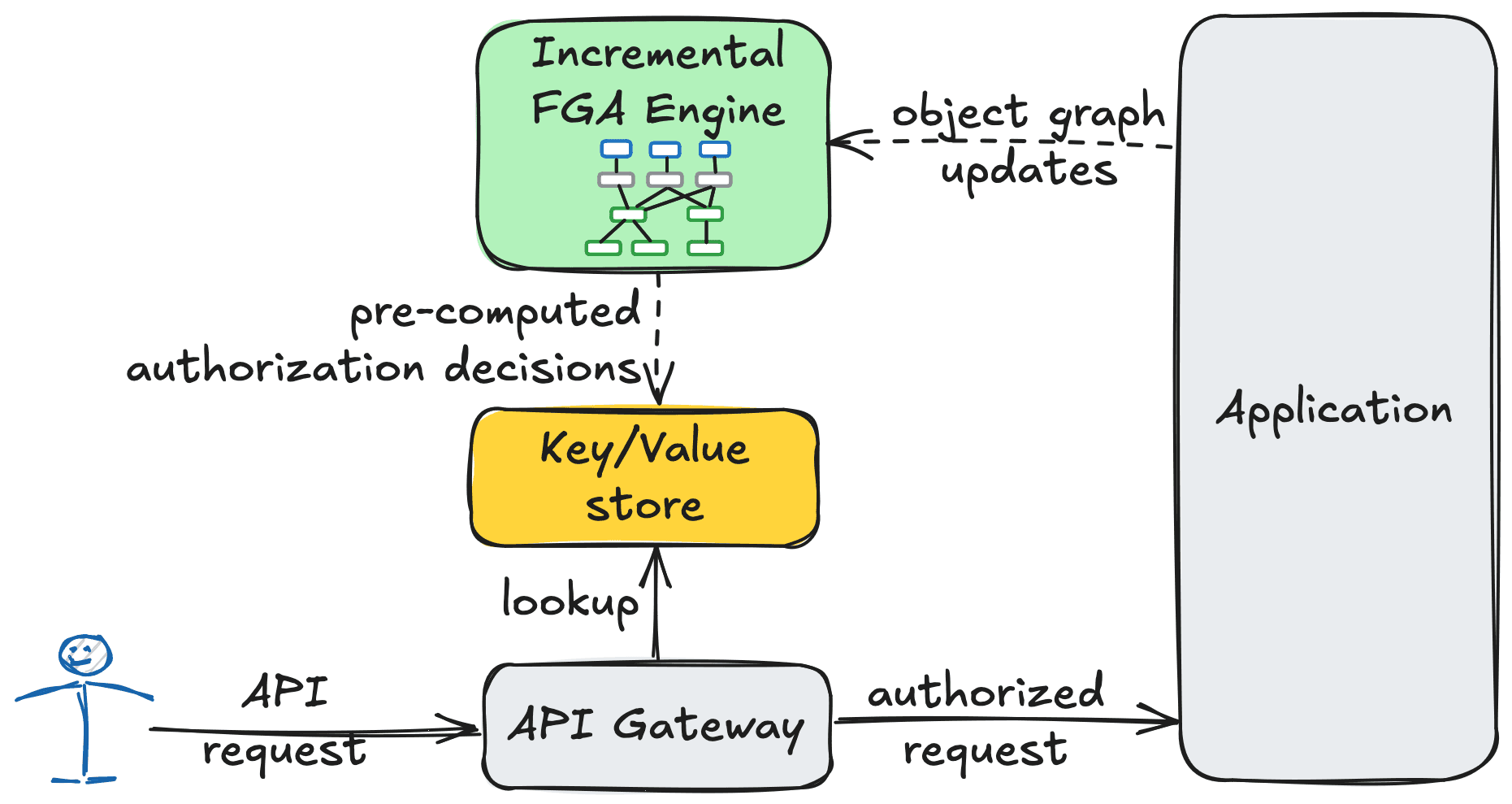
How does one build such a system without sending their cloud bill through the roof? In this blog we show how this can be achieved by turning the problem on its head. Instead of evaluating every individual authorization request from scratch, we precompute all relevant authorization decisions ahead of time, turning authorization requests into simple key/value lookups.
To make this work, we need a way to keep precomputed results up to date. The object graph changes all the time, potentially invalidating previously computed authorization decisions. To handle these changes, we need a compute layer that can update its outputs incrementally, without full recomputation. We use Feldera, our incremental SQL engine, to this end. Feldera supports incremental evaluation of arbitrary SQL queries, including mutually recursive queries--a crucial feature for implementing iterative graph traversal in SQL.

In the rest of this article, we introduce the basics of FGA and implement a high-performance FGA engine using only a few lines of SQL.
FGA basics
Object graph
An FGA policy is defined over an object graph, where nodes represent system objects and edges capture the relationships between these objects. Consider a simple file management service as an example. This application works with three types of objects: users, user groups, and files (for simplicity, we model files and folders using a single object type) connected by the following relationships:
member- a relationship between a user and a group.parent- a relationship between files that defines the folder hierarchy.editor- a relationship between a group and a file that gives the group the permission to read or write the file.viewer- a relationship between a group and a file that gives the group the permission to read the file.
We use relationship(object1, object2) notation for relationships, e.g., member(alice, engineering), parent(folder1, file1), editor(admins, folder1), etc.Here is an example object graph that shows several users, groups, and files. Note that objects can have attributes, e.g., is_banned.

Rules
An FGA policy consists of rules that derive new relationships from the object graph. A rule consists of prerequisites that must hold for the rule to fire and the derived clause that holds if the prerequisites are satisfied.
We define the following derived relationships in our file manager example:
group-can-read(group, file)-groupis allowed to readfile.group-can-write(group, file)-groupis allowed to writefile.user-can-read(user, file)-useris allowed to readfile.user-can-write(user, file)-useris allowed to writefile.
These relationships are governed by the following rules:
- Rule 1:
editor(group, file) -> group-can-write(group, file)- if a group is an editor of a file, it can write this file. - Rule 2:
group-can-write(group, file1) and parent(file1, file2) -> group-can-write(group, file2)- if a group can write a file, then it can write any of its children. - Rule 3:
viewer(group, file) -> group-can-read(group, file)- if a group is a viewer of a file, then it can read this file. - Rule 4:
group-can-write(group, file) -> group-can-read(group, file)- the write permission to a file implies the read permission to the same file. - Rule 5:
group-can-read(group, file1) and parent(file1, file2) -> group-can-read(group, file2)- if a group can read a file,
then it can read any of its children. - Rule 6:
member(user, group) and group-can-write(group, file) and (not user.is_banned) -> user-can-write(user, file)- if a user is a member of a group that can write a file and the user is not banned, then the user can write the file. - Rule 7:
member(user, group) and group-can-read(group, file) and (not user.is_banned) -> user-can-read(user, file)- if a user is a member of a group that can read a file and the user is not banned, then the user can read the file.
Given these rules, we can derive the following access permissions to file `f1` from the example object graph above:
user-can-write(emily, f1)user-can-read(emily, f1)user-can-write(irene, f1)user-can-read(irene, f1)
FGA as an incremental computation problem
Evaluating authorization rules is an expensive affair. Whenever a user tries to perform an action on a resource, the FGA engine must check that there exists a path in the object graph between the user and the resource, that complies with authorization rules. For example, the red path in the graph above shows the derivation of the user-can-write(emily, f1) relationship. The worst-case complexity of finding a path in a graph is proportional to the size of the graph (the number of nodes + the number of edges).
And that's just for one authorization check! In a large-scale application, the system may need to handle thousands of such checks every second, within a latency budget of tens of milliseconds per check.
Incremental computation offers an elegant solution to this challenge. Instead of evaluating authorization decisions from scratch for every request, the idea is to precompute all authorization decisions in advance and store them in a key-value store, reducing runtime authorization checks to simple, efficient lookups. As the object graph evolves, incremental computation ensures that only rule derivations affected by the change are updated, avoiding full recomputation. An efficient incremental query engine like Feldera can update the computation within milliseconds after the object graph changes even for very large graphs, making sure that runtime authorization checks reflect the current state of the system.
Building an incremental FGA engine in SQL
It's time to write some SQL! Let's implement the file manager authorization model using Feldera. The implementation described here is available as a pre-packaged example in the Feldera online sandbox as well as in your local Feldera installation.
Modeling the object graph
We start with modeling the three object types—users, groups, and files—as SQL tables:
create table users (
id bigint not null primary key,
name string,
is_banned bool
) with ('materialized' = 'true');
create table groups (
id bigint not null primary key,
name string
) with ('materialized' = 'true');
create table files (
id bigint not null primary key,
name string,
-- Parent folder id; NULL for a root folder.
parent_id bigint
) with ('materialized' = 'true');Note that the parent_id field models the parent relationship between files.
Next, we model member, editor, and viewer relationships:
-- Member relationship models user membership in groups.
create table members (
id bigint not null primary key,
user_id bigint not null,
group_id bigint not null
) with ('materialized' = 'true');
-- Editor relationship between a group and a file that gives the group the permission
-- to read or write the file.
create table group_file_editor (
group_id bigint not null,
file_id bigint not null
) with ('materialized' = 'true');
-- Viewer relationship between a group and a file that gives the group the permission to read the file.
create table group_file_viewer (
group_id bigint not null,
file_id bigint not null
) with ('materialized' = 'true');Implementing rules
We are now ready to implement derived relationships. We start with the group-can-write relationship defined by the following two rules.
- Rule 1:
editor(group, file) -> group-can-write(group, file). - Rule 2:
group-can-write(group, file1) and parent(file1, file2) -> group-can-write(group, file2).
In Rule 2 group-can-write appears on both sides of the implication, indicating that this is a recursive relationship. Rule 1 specifies the base case of recursions: a group has write access to all files for which it is an editor. Rule 2 defines the recursive step: write permissions propagate from a file to all its children. We implement these rules as a recursive SQL view:
declare recursive view group_can_write (
group_id bigint not null,
file_id bigint not null
);
create materialized view group_can_write as
-- Rule 1: editor(group, file) -> group-can-write(group, file).
(
select group_id, file_id from group_file_editor
)
union all
-- Rule 2: group-can-write(group, file1) and parent(file1, file2) -> group-can-write(group, file2).
(
select
group_can_write.group_id,
files.id as file_id
from
group_can_write join files on group_can_write.file_id = files.parent_id
);Note how in writing these queries we do not need to worry about incremental evaluation. As a developer, you simply specify how new relationships can be derived from existing ones. The engine takes care of incrementalization fully automatically.
We continue implementing the remaining rules 3 through 7 in a similar fashion. Refer to our FGA tutorial for the complete code.
Kicking the tires
Copy the complete SQL code for the file manager example to the Feldera Web Console. Start the pipeline and populate the object graph to match the example above by issuing the following ad hoc queries:
insert into users values
(1, 'emily', false),
(2, 'irene', false),
(3, 'adam', true);
insert into groups values
(1, 'engineering'),
(2, 'it'),
(3, 'accounting');
insert into files values
(1, 'designs', NULL),
(2, 'financials', NULL),
(3, 'f1', 1),
(4, 'f2', 1),
(5, 'f3', 2);
insert into members values
(1, 1, 1), -- emily is in engineering
(2, 2, 2), -- irene is in IT
(3, 3, 3); -- adam is in accounting
insert into group_file_editor values
(1, 1), -- 'engineering' can edit 'designs'
(2, 1), (2, 2), -- 'it' can edit 'designs' and 'financials'
(3, 2); -- 'accounting' can edit 'financials'.
insert into group_file_viewer values
(3, 1); -- 'accounting' can view 'designs'.We can now validate the output of the program, e.g.:
select
users.name as user_name,
files.name as file_name
from
user_can_read
join users on users.id = user_can_read.user_id
join files on files.id = user_can_read.file_id;| user_name | file_name |
| emily | designs |
| irene | designs |
| irene | financials |
| irene | f3 |
| emily | f1 |
| irene | f1 |
| emily | f2 |
| irene | f2 |
As expected, emily, being a member of engineering, has read access to all files under the designs folder, while irene, a member of it, can read files under both designs and financials.
Next we make an incremental change to the object graph, adding emily to the it group:
insert into members values (4, 1, 2);Running the select query above will return two additional rows:
| user_name | file_name |
| emily | financials |
| emily | f3 |
Running at full speed
The Feldera sandbox features the above program configured with a data generator that builds a random object graph with 1,000 users, 100 groups, 100 top-level folders, 1,000 sub-folders, and 100,000 files randomly distributed across the sub-folders. The generator runs continuously, dynamically updating the random set of 100,000 files. Additionally, it continuously modifies user group memberships.
Running on a MacBook Pro with M3 Max CPU, this program achieves sustained throughput of 115K updates/s, meaning that it processes 115K object graph changes/s and updates **all derived relationships** every second.
Note that the datagen in the sandbox is equipped with a rate limiter that restricts throughput to 2,000 events per second to conserve shared sandbox resources.
There's no free lunch!
Incremental computation unlocks massive performance improvements: instead of performing an expensive graph traversal for each authorization request, all computation is done ahead of time in response to changes in the object graph. The engine processes these changes by calculating updates to the set of derived relationships, in time proportional to the size of the update.
These improvements come at the cost of the extra storage the incremental query engine uses to do its job. Specifically, it must store all relationships derived from the object graph, which can require storage quadratic in the number of nodes in the graph. As a concrete example, in a system with 1M users and 1M public files, the policy engine could derive 10^12 user-can-read relationships.
Therefore, a scalable FGA system must take care to only derive a subset of relationships that can be accessed by authorization checks performed by the system. For example, only users who are logged into the system can issue authorization requests; hence we only need to consider currently active users in the computation. See our detailed tutorial for a more detailed discussion and a concrete example of this type of optimization.
Implementing a dynamic FGA model
What if we wanted to allow not only the object graph, but also the access control model itself to change at runtime? For instance, consider building a generic FGA platform like OpenFGA, where users can define new object types, relationships, and rules. In the file manager example, we may want to add a new type of relationship, owner, which gives the user authority to permanently delete a file from the system.
Turns out, this can also be expressed as an incremental SQL program. The key idea is to model FGA rules as relational data instead of hard-coding them as SQL queries. See our complete tutorial for details.
Takeaways
Separation of concerns is how computer scientists get things done. In this article, we isolated the problem of efficiently evaluating FGA rules and reframed it as an incremental compute problem. We used a specialized incremental compute tool to solve this problem, achieving outstanding single-node performance with minimal development effort: all we had to do is write a few simple SQL queries.
Whether you are adding a flexible authorization layer to your application or building a general-purpose policy framework, you may want to consider using an incremental query engine like Feldera as your compute engine. Two features of Feldera make it ideal for this purpose:
- Incremental query evaluation enables Feldera to handle changes to the object graph or the FGA model in real-time by avoiding complete recomputation.
- Support for mutually recursive views allows naturally capturing iterative
graph traversal with recursive queries.
Other articles you may like
Database computations on Z-sets
How can Z-sets be used to implement database computations
Implementing Batch Processes with Feldera
Feldera turns time-consuming database batch jobs into fast incremental updates.
Feldera: three tools for the price of one
Feldera is not just a database engine. Feldera SQL is in some respects substantially more powerful than standard SQL, enabling new use cases.