Computing with changes

Incremental computation

Incremental computation is a computation that reuses results that were previously computed.

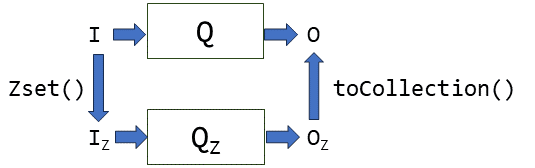
Let us assume you have a program P that is given an input I and
produces an output O:

Now let's change the input by modifying it with some change, which
we denote by ΔI:

We would like to avoid computing the entire output again, and ideally reuse the previously computed $O$ and only adjust it by a change ΔO. This would be great especially if the output doesn't change much.

This sounds nice, but is very vague. To make this work we have to explain what a change is (what we denoted by Δ) and what it means to change something (what we denoted by +). This may be difficult to define precisely for an arbirary computation, but it works very well in some important domains.

Changes in documents

If you have used change tracking in Microsoft Word, you have encountered a version of changes. Here is a screenshot of Word showing changes to short document:

Word keeps track of the changes by looking at your keystrokes and recording what is being deleted (shown with a strikethrough) or inserted (shown as underlined). Notice that Word doesn't attempt to show the minimal changes performed -- which could be shown just by the deletion of the apostrophe `'` in it's, but it rather mirrors the actions you have performed to change the document.

Change tracking is such a useful feature in Word because it allows readers to avoid reading a whole edited document to discover what has changed. In general: Change tracking is mostly useful when changes are expected to be
small compared to the modified object

Changes in programs

Most programmers have encountered a natural notion of change: since programs evolve constantly, one often speaks about the changes between two versions of a program. Important activities of programmers, such as code reviews, often only look at changes in programs.

There are specific tools, like diff which compute changes between text files. Here is an example from the above Wikipedia page:

$ diff original new
0a1,6
> This is an important
> notice! It should
> therefore be located at
> the beginning of this
> document!
>
11,15d16
< This paragraph contains
< text that is outdated.
< It will be deleted in the
< near future.
17c18
< check this dokument. On
---
> check this document. On

Here both original and new are text files. The diff tool operates on lines, and shows how lines in one file have to be modified to generate the second file. The tool diff describes the difference as a set of additions, (abbreviated a), deletions (d) and changes (c). The above output shows that to change file original into new one has to add 6 lines at starting from line 0, delete lines 11 to 15, and then replace line 17. The < sign points to lines in the left file (original), while the > sign points to lines in the right file.

Notice that the difference between two files can be described in multiple ways: another way would be to delete everything in the first file and then add everything in the second file. The diff tool tries to find a small set of changes, modifying as few lines as possible. Also, unlike Word, `diff` does not show character changes, only full line changes.

Also, notice that diff changes are described as being composed of multiple simpler changes: the example contains one insertion, one deletion, and one modification.

diff can compare not only two files but it can also compare multiple files at once. Entire files can be inserted, deleted, renamed, or changed individually. Another tool, patch can use such a description to convert a set of old file versions into a set of newer ones. Changes can be hierarchical: changes to complex objects can be described from changes to simpler ones.

Data and changes

Notice that we are dealing with two different kinds of structures: the changed objects (e.g., files), and the changes between objects (deltas, or diffs). (One can store a change in a text file, but it's really a different object.)

Let's call these two data structures D for data, and Δ for changes. First we have a diff operation D - D -> Δ: where we use minus for the diff. The diff between two data values is a change.

We also have an inverse operation: $D + \Delta \to D$, which changes some data by applying a change. There is also a notion of an empty change, which is the difference between two identical data values.

Changing numbers

In some circumstances the data and the changes can look similar. Consider the case of a bank account. The value of the account is a dollar amount -- a number. At the end of each month we get a bank statement describing the change in the value of the account: also a number. For bank accounts the changes can be both positive and negative but, unless you have overdraft protection, the amounts are always positive.

This is another important lesson: applying a change to a valid data value may not produce another valid data value. Removing $10 from your bank account is a permitted change if you have $20, but not if you have only $5 left. So the validity of a change cannot be evaluated in isolation, you have to know *what* is being changed. Only the application domain can decide that.

For this case the structures D and Δ are identical: you can represent both the data and the changes as numbers (but you must include negative numbers if you want to represent all possible changes). Empty data and empty changes are both the number zero. This is very convenient. We will show in a future blog post that we can take advantage of this nice property even when we don't handle just numbers.

Databases and changes

Databases are an application domain where changes are actually central. Changes appear in databases in two guises, which look very dissimilar superficially: transactions and change data capture; we describe these in more details below. These forms appear superficially dissimilar and historically treated separately, but their fundamental similarity leads us to believe that in the future
they should be unified.

(There is yet another way that changes appear in databases, in the guise of Incremental View Maintenace; we reserve a future blog post to discuss about this kind of changes.)

Transactions

A database is a set of tables. To simplify the discussion, let us assume that the database schema does not change - i.e., the set of tables is fixed. (Schema changes can be handled as well, but let's keep this discussion simple.) A change to the database can be described by a set of changes, one to each table, similar to the way a patch contains changes to multiple files.

What is a change to a table? It is a set of insertions, deletions, or updates to the table's rows. Every time you execute a SQL statement such as INSERT:

INSERT INTO PEOPLE VALUES('John', 2)

you are in fact describing a change to that table (PEOPLE, in this example). These are the simplest changes that one can apply to a table.

Similar to the way a diff change is described by multiple simple changes, in a database real changes are described by transactions which group multiple changes together.

This is an important concept, so let us highlight it:

Transactions describe database changes.

Transactions do many other things, like isolation, durability, etc, but here we care only about their ability of describing changes that are applied together.

As we observed previously, it is possible to describe changes that are not always valid, such as deleting a row that doesn't exist from a table, or inserting a row that duplicates a primary key. Attempting to execute such a change in a transaction will usually result in the entire transaction being aborted.

Change data capture

There are many applications where one would like to know what has changed in a database. Companies are developing sophisticatedproducts for this purpose, that are sold under the name Change Data Capture, or CDC. A typical application of CDC is mirroring (copying) the data of a database into a remote database for disaster recovery. You don't want to periodically copy all the data, but you would rather send the changes continuously, as they happen. So you install a CDC system in the source database, which sends the changes to the second database, which applies them to its contents.

CDC describes database changes.

So a diagram of the system looks roughly like this:

Notice that transactions and CDC really have the same definition. In practice, however, they work in completely different ways. Transactions are expressed using SQL statements grouped into programs, while CDC is usually expressed in a complex format (perhaps encoded as JSON), which describes also the changes in terms of simple changes. Recovering transactions from CDC is usually a very involved process.

We believe that, in ideal world, CDC and changes described by transactions should be described in the same language. But legacy systems are very hard to change, so it may be a long time before this happens. But it is still very important to understand this conceptual relationship. In future articles we will show why unifying these two concepts can have some unexpected benefits.

But first, we discuss Z-Sets in the next post: A efficient data-structure to represent changes (which also has some nice mathematical properties for computation).